6 minutes
Hybrid Search of Pinecone
1. Brief
A summery of paper An analysis of Fusion Functions for Hybrid Retrieval and the following three articles.
[1]. Introducing support for sparse-dense embeddings for better search results
[2]. Sparse-dense embeddings, keyword-aware semantic search, Concepts
[3]. Ecommerce Hybrid Search, Hybrid Search Case
[4]. Tao Chen, Mingyang Zhang, Jing Lu, Michael Bendersky, and Marc Najork. 2022. Out-of-Domain Semantics to the Rescue! Zero-Shot Hybrid Retrieval Models. In Advances in Information Retrieval: 44th European Conference on IR Research, ECIR 2022, Stavanger, Norway, April 10-14, 2022, Proceedings, Part I (Stavanger, Norway). 95-110.
[5]. Shuai Wang, Shengyao Zhuang, and Guido Zuccon. 2021. BERT-Based Dense Retrievers Require Interpolation with BM25 for Effective Passage Retrieval. In Proceedings of the 2021 ACM SIGIR International Conference on Theory of Information Retrieval (Virtual Event, Canada). 317-324.
2. About the paper
What does the paper contribute? The paper study hybrid search in text retrieval where lexical and semantic search are fused together with the intuition that the two are complementary in how they model relevance.
convex combination(CC) of lexical and semantic scores, as well as the Reciprocal Rank Fusion(RRF) method
What’s retrieval? Retrieval is the first stage in a multi-stage ranking system, where the objetive is to find the top-k set of documents, that are the most relevant to a given query q, from a large collection o f documents $D$. There’re 2 major research questions: a)How do we measure the relevance between a query q and a document $d\in{D}$; and b) How do we fine the top-k documents according to a given similarity metric efficiently.
What is lexical search? Early methods model text as a Bag of Words(BoW) and compute the similarity of two pieces of text using a statistical measure such as the term frequency-inverse document frequency(TF-IDF) family, with BM25 being its most promient member.
The paper refers to retrieval with a BoW model as lexical search and the similarity scores computed by such a system as lexical scores, also known as key-word matching.
Actually in the artical [1], pinecone thinks new models like SPLADE, uniCOIL are better than BM25.
Since then, progress continues to be made with alternative sparse models (e.g. SPLADE, uniCOIL), leading to even more relevant results than BM25.
Lexical search is simple, efficient, “zero-shot”, and generally effective, but
-
Because BM25, like other lexical scoring fucntions, insists on an exact match of terms, even a slight typo chan throw the function off. It’s susceptible to the vocabulary mismatch problem and,
-
It doesn’t take into account the semantic similarity of queries and documents.
What is semantic search? Both the issues of lexical search can be remedied by pre-trained language models such as BERT. Semantics are what deep learning moduls excellent at. To learn a vector representation of quries and documents from pre-trained language models such as BERT does capture their semantics, and thereby, reduc top-k retrieval to the problem of finding k nearest neighbors in the resulting vector space.
The paper refers to this method as semantic search and the similarity scores computed by such a system as semantic scores.
Semantics search has limitations, that when applied to out-of-domian datasets, their performance is often worse than BM25.
What is hybrid search? Thus it’s natural to consider a hybrid approch where lexical and semantic similarities both contribute to the makeup of final retrieved list.
For a query $q$ and ranked lists of documents $R_{LEX}$ and $R_{SEM}$ retrieved separatedly by lexical and semantic search systems respectively, the task is to construct a final ranked list $R_{FUSION}$ so as to improve retrieval quality. This is often referred to as hybrid search.
The paper says that hybrid search does lead to meaningful gains in retrieval quality, especially when applied to out-of-domain datasets, inreference of papers [4, 5].
Out-of-domain means settings in which the semantic retrieval component uses a model that was not trained or fine-tuned on the target dataset.
Convex combination One common approach is to linearly combine lexical and semantic scores. If $f_{LEX}(q, d)$ dne $f_{SEM}(q, d)$ represent the lexical and semantic scores of document $d$ with respect to query $q$, then a linear (convex) combination is expressed as:
$f_{CONVEX} = \alpha f_{SEM} + (1 - \alpha) f_{LEX}$ where $0 \le \alpha \le 1$
Because lexical scores (such as BM25) and semantic scores (such as dot product) may be unbounded, often they are normalized with min-max scaling prior to fushion.
RRF Reciprocal Rank Fusion is another way to fusion.
What EXACTLY does this paper do in compare with [4]? [4] addresses how various hybrid methods perform relative to one another in an empirical study. This paper re-examine [4]’s findings and anyalyze why these methods work and what contributes to their relative performance.
In summary, this paper in-depth exam the fusion functions and their behaiover, more specificly two functions: CC and RRF.
What’s a well-behaved fusion funtion?
Addressed by the paper:
- Monotonicity
- Homogeneity
- Boundedness
- Lipschitz Continuity
- Interpretability and Sample Efficiency
What’s the conclusion? That convex combination formulation is theoretically sound, empirically effective, sample-effeicient, and robust to domain shift. and unlike the parameters in RRF, the parameter(s) of convex function are highly interpretable and, if no training samples are available, can be adjusted to incorporate domain knowledge.
The paper believes that a convex combination with theoretical minimum-maximum normalization (TM2C2) indeed enjoys properties that are important in a fusion function. Its parameter can be tuned sample-efficiently or set to a reasonable value based on domain knowledge. In the paper’s experiments, the range $\alpha \in [0.6, 0.8]$ can consistently lead to improvements
3. Sparse-dense embeddings: from theory to engineering
Sparse vs. Dense
Pinecone says in article [1] that vectors generated by BoW models are sparse vector, for they have large dimension(e.g. 100,000) where only a small fraction of its entries are non-zero, used for texical search.
[0.1, 0, 0, 0, 0, 0, ..., 0.3, ..., 0]
When used for keywords search, each sparse vector represents a document. The dimensions represent workds from a dictionary, and the values represent the importance of these workds in the document. Keyword search algorithms like BM25 algorithm compute the relevance of text documents based on the number of keyword matches, their frequency, and other factors.
Sparse vector’s distance is calculated by doc product(IP) metric.
Vectors generated by ML models like SBERT are dense vector, they are vectors of fixed dimensions, typically between 100-1000, where every entry is almost always non-zero. They may represent the learned semantic meaning of texts, used for semantic search.
In Pinecone, each vector consists of dense vector values and, optionally, sparse vector values as well. Pinecone does not support vectors with only sparse values.
upsert_response = index.upsert(
vectors=[
{'id': 'vec2',
'values': [0.2, 0.3, 0.4],
'metadata': {'genre': 'action'},
'sparse_values': {
'indices': [15, 40, 11],
'values': [0.4, 0.5, 0.2]
}}
],
namespace='example-namespace'
)
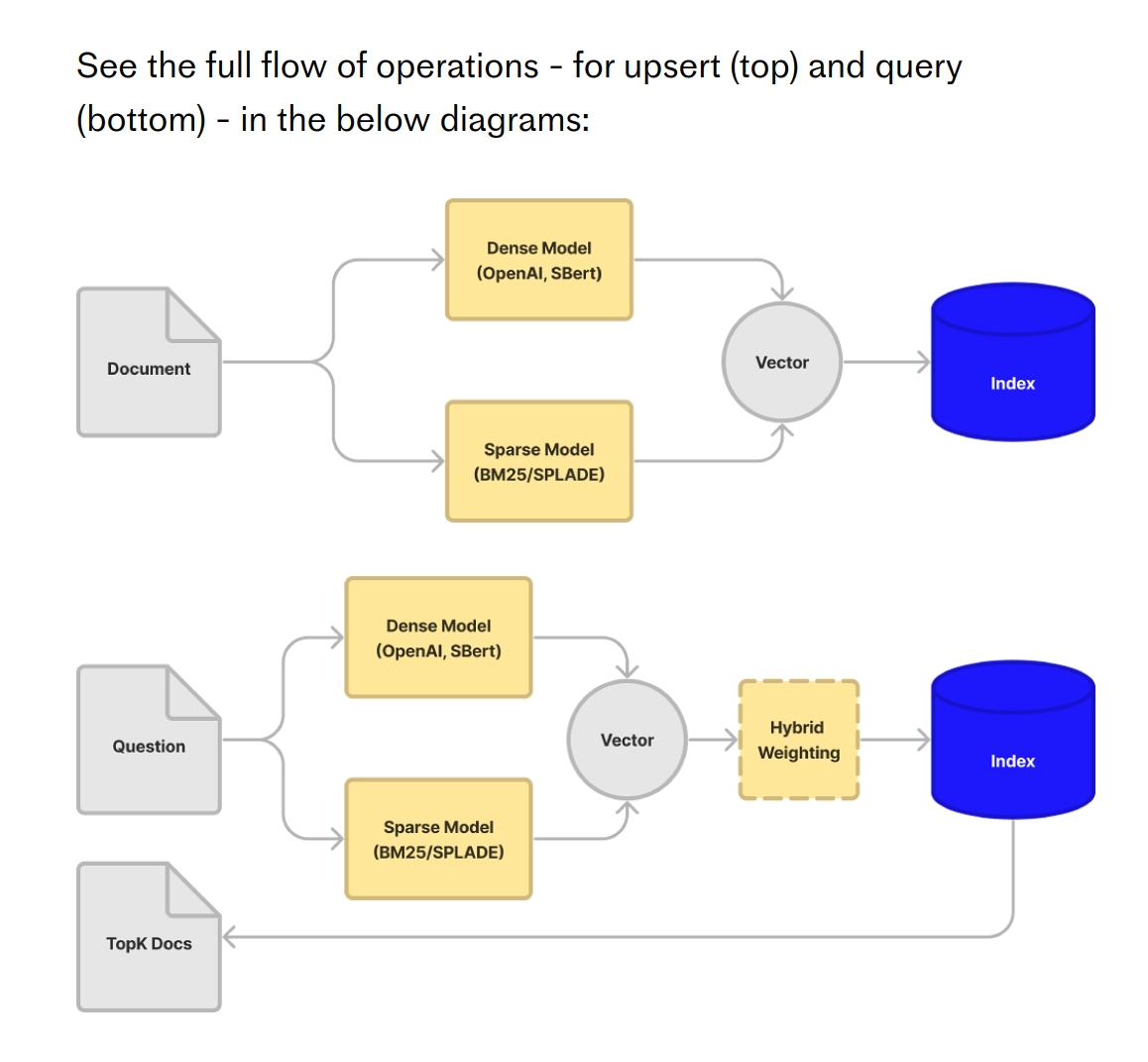
So the full flow of operations are:
References
Some useful reading resources about SPLADE
1 T. Formal, B. Piwowarski, S. Clinchant, SPLADE: Sparse Lexical and Expansion Model for First Stage Ranking (2021), SIGIR 21
2 T. Formal, C. Lassance, B. Piwowarski, S. Clinchant, SPLADE v2: Sparse Lexical and Expansion Model for Information Retrieval (2021)
3 SPLADE for Sparse Vector Search Explained